Tutorial: setting the hyperparameters¶
In this demo, we’ll reproduce the analysis for Figure 5.6 in Chapter 5 of Rasmussen & Williams (R&W). The data are measurements of the atmospheric CO2 concentration made at Mauna Loa, Hawaii (Keeling & Whorf 2004). The dataset is said to be available online but I couldn’t seem to download it from the original source. Luckily the statsmodels package includes a copy that we can load as follows:
import numpy as np
import statsmodels.api as sm
data = sm.datasets.get_rdataset("co2").data
t = np.array(data.time)
y = np.array(data.co2)
These data are plotted in the figure below:
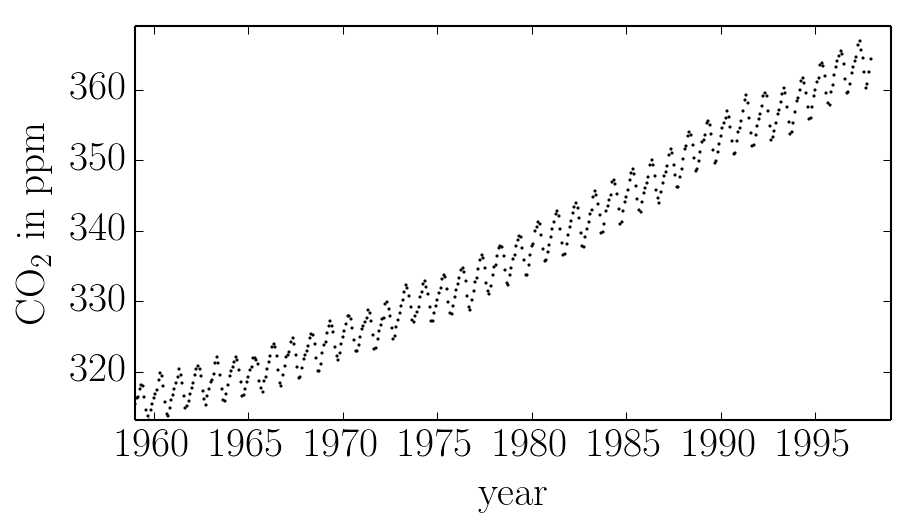
In this figure, you can see that there is periodic (or quasi-periodic) signal with a year-long period superimposed on a long term trend. We will follow R&W and model these effects non-parametrically using a complicated covariance function. The covariance function that we’ll use is:
where
We can implement this kernel in George as follows (we’ll use the R&W results as the hyperparameters for now):
from george import kernels
k1 = 66.0**2 * kernels.ExpSquaredKernel(67.0**2)
k2 = 2.4**2 * kernels.ExpSquaredKernel(90**2) * kernels.ExpSine2Kernel(2.0 / 1.3**2, 1.0)
k3 = 0.66**2 * kernels.RationalQuadraticKernel(0.78, 1.2**2)
k4 = 0.18**2 * kernels.ExpSquaredKernel(1.6**2) + kernels.WhiteKernel(0.19)
kernel = k1 + k2 + k3 + k4
Optimization¶
If we want to find the “best-fit” hyperparameters, we should optimize an objective function. The two standard functions (as described in Chapter 5 of R&W) are the marginalized ln-likelihood and the cross validation likelihood. George implements the former in the GP.lnlikelihood() function and the gradient with respect to the hyperparameters in the GP.grad_lnlikelihood() function:
import george
gp = george.GP(kernel, mean=np.mean(y))
gp.compute(t)
print(gp.lnlikelihood(y))
print(gp.grad_lnlikelihood(y))
The gradient is taken with respect to the vector property of the kernel so this is what you want to fit for. For most kernels the vector is actually the logarithm of the hyperparameters (see the discussion in Implementation Details). We’ll use a gradient based optimization routine from SciPy to fit this model as follows:
import scipy.optimize as op
# Define the objective function (negative log-likelihood in this case).
def nll(p):
# Update the kernel parameters and compute the likelihood.
gp.kernel[:] = p
ll = gp.lnlikelihood(y, quiet=True)
# The scipy optimizer doesn't play well with infinities.
return -ll if np.isfinite(ll) else 1e25
# And the gradient of the objective function.
def grad_nll(p):
# Update the kernel parameters and compute the likelihood.
gp.kernel[:] = p
return -gp.grad_lnlikelihood(y, quiet=True)
# You need to compute the GP once before starting the optimization.
gp.compute(t)
# Print the initial ln-likelihood.
print(gp.lnlikelihood(y))
# Run the optimization routine.
p0 = gp.kernel.vector
results = op.minimize(nll, p0, jac=grad_nll)
# Update the kernel and print the final log-likelihood.
gp.kernel[:] = results.x
print(gp.lnlikelihood(y))
Warning
An optimization code something like this should work on most problems but the results can be very sensitive to your choice of initialization and algorithm. If the results are nonsense, try choosing a better initial guess or try a different value of the method parameter in op.minimize.
After running this optimization, we find a final ln-likelihood of -82.46 (slightly better than the result in R&W) and the following parameter values:
| result | R&W | |
|---|---|---|
| \(\theta_{1}\) | 1183.17 | 4356.00 |
| \(\theta_{2}\) | 1740.98 | 4489.00 |
| \(\theta_{3}\) | 10.35 | 5.76 |
| \(\theta_{4}\) | 40248.23 | 8100.00 |
| \(\theta_{5}\) | 0.99 | 1.18 |
| \(\theta_{6}\) | 1.00 | 1.00 |
| \(\theta_{7}\) | 0.04 | 0.44 |
| \(\theta_{8}\) | 3.48 | 0.78 |
| \(\theta_{9}\) | 0.02 | 1.44 |
| \(\theta_{10}\) | 0.19 | 0.03 |
| \(\theta_{11}\) | 0.95 | 2.56 |
| \(\theta_{12}\) | 0.03 | 0.19 |
We can plot our prediction of the CO2 concentration into the future using our optimized Gaussian process model by running:
x = np.linspace(max(t), 2025, 2000)
mu, cov = gp.predict(y, x)
std = np.sqrt(np.diag(cov))
and this gives a result just like Figure 5.6 from R&W:

Sampling & Marginalization¶
The prediction made in the previous section take into account uncertainties due to the fact that a Gaussian process is stochastic but it doesn’t take into account any uncertainties in the values of the hyperparameters. This won’t matter if the hyperparameters are very well constrained by the data but in this case, many of the parameters are actually poorly constrained. To take this effect into account, we can apply prior probability functions to the hyperparameters and marginalize using Markov chain Monte Carlo (MCMC). To do this, we’ll use the emcee package.
First, we define the probabilistic model:
def lnprob(p):
# Trivial improper prior: uniform in the log.
if np.any((-10 > p) + (p > 10)):
return -np.inf
lnprior = 0.0
# Update the kernel and compute the lnlikelihood.
kernel.pars = np.exp(p)
return lnprior + gp.lnlikelihood(y, quiet=True)
In this function, we’ve applied a prior on every parameter that is uniform in the natural log between -10 and 10. The quiet argument in the call to GP.lnlikelihood() means that that function will return -numpy.inf if the kernel is invalid or if there are any linear algebra errors (otherwise it would raise an exception).
Then, we run the sampler (this will probably take a while to run if you want to repeat this analysis):
import emcee
# You need to compute the GP once before starting. Then the sample list
# will be saved.
gp.compute(t)
# Set up the sampler.
nwalkers, ndim = 36, len(kernel)
sampler = emcee.EnsembleSampler(nwalkers, ndim, lnprob)
# Initialize the walkers.
p0 = [np.log(kernel.pars) + 1e-4 * np.random.randn(ndim)
for i in range(nwalkers)]
print("Running burn-in")
p0, _, _ = sampler.run_mcmc(p0, 2000)
print("Running production chain")
sampler.run_mcmc(p0, 2000)
After this run, you can plot 50 samples from the marginalized predictive probability distribution:
import matplotlib.pyplot as pl
x = np.linspace(max(t), 2025, 250)
for i in range(50):
# Choose a random walker and step.
w = np.random.randint(chain.shape[0])
n = np.random.randint(2000, chain.shape[1])
gp.kernel.pars = np.exp(chain[w, n])
# Plot a single sample.
pl.plot(x, gp.sample_conditional(y, x), "k", alpha=0.3)
This should give you a figure similar to this one:

Comparing this to the same figure in the previous section, you’ll notice that the error bars on the prediction are now substantially larger than before. This is because we are now considering all the predictions that are consistent with the data, not just the “best” prediction. In general, even though it requires much more computation, it is more conservative (and honest) to take all these sources of uncertainty into account.