Getting started¶

Installation¶

You can install the most recent stable version of George using PyPI or the development version from GitHub.

Prerequisites¶

Whichever method you choose, you’ll need to make sure that you first have Eigen installed. On Linux:

sudo apt-get install libeigen3-dev

On Mac:

brew install eigen

Note

Chances are high that George won’t work on Windows right now because it hasn’t been tested at all but feel free to try it out at your own risk!

You’ll also need a working scientific Python installation (including NumPy and SciPy). I recommend the Anaconda distribution if you don’t already have your own opinions.

Stable Version¶

The simplest way to install the most recent stable version of George is using pip:

pip install george

If you installed Eigen in a strange place, specify that location by running (sorry to say that it’s pretty freaking ugly):

pip install george \
    --global-option=build_ext \
    --global-option=-I/path/to/eigen3

Development Version¶

To get the source for the development version, clone the git repository and checkout the required HODLR submodule:

git clone https://github.com/dfm/george.git
cd george
git submodule init
git submodule update

Then, install the package by running the following command:

python setup.py install

If installed Eigen in a non-standard location, you can specify the correct path using the install command:

python setup.py build_ext -I/path/to/eigen3 install

Testing¶

To run the unit tests, install nose and then execute:

nosetests -v george.testing

All of the tests should (of course) pass. If any of the tests don’t pass and if you can’t sort out why, open an issue on GitHub.

A Simple Example¶

The following code generates some fake data (from a sinusoidal model) with error bars:

import numpy as np

# Generate some fake noisy data.
x = 10 * np.sort(np.random.rand(10))
yerr = 0.2 * np.ones_like(x)
y = np.sin(x) + yerr * np.random.randn(len(x))

Then, we’ll choose a simple kernel function (see Kernels for some other choices) and compute the log-likelihood of the fake data under a Gaussian process model with this kernel:

import george
from george.kernels import ExpSquaredKernel

# Set up the Gaussian process.
kernel = ExpSquaredKernel(1.0)
gp = george.GP(kernel)

# Pre-compute the factorization of the matrix.
gp.compute(x, yerr)

# Compute the log likelihood.
print(gp.lnlikelihood(y))

Finally, we can compute the predicted values of the function at a fine grid of points conditioned on the observed data. This prediction will be an \(N_\mathrm{test} \times N_\mathrm{test}\) multivariate Gaussian (where \(N_\mathrm{test}\) is the number of points in the grid) with mean mu and covariance cov:

t = np.linspace(0, 10, 500)
mu, cov = gp.predict(y, t)
std = np.sqrt(np.diag(cov))

This should result in a constraint that looks something like:

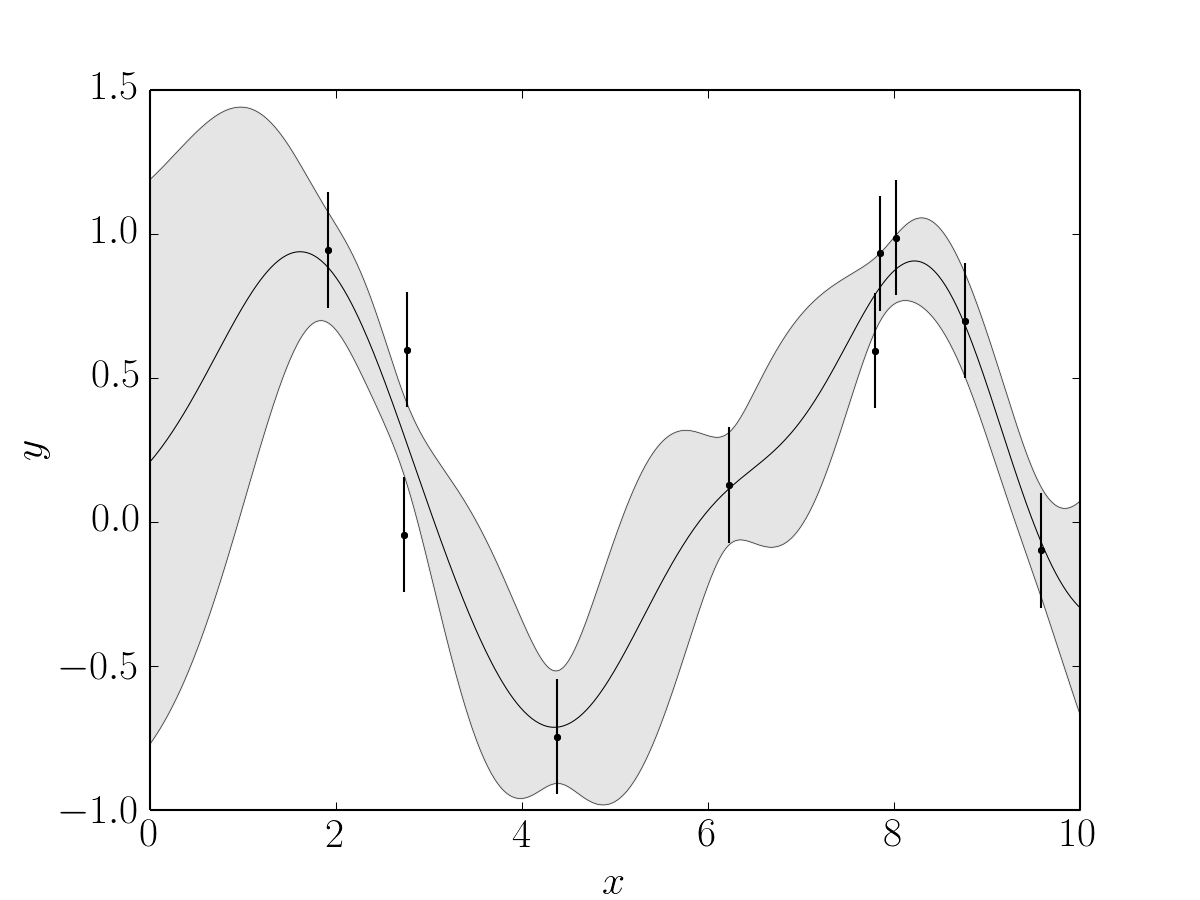
where the points with error bars are the simulated data and the filled gray patch is the mean and standard deviation of the prediction.